An object falling from rest from a height h would have a velocity
upon hitting the ground. This is with no air resistance present. With air resistance the velocity is smaller (part of the lost kinetic energy is given up to heat of friction). In fact, if h is large enough, the object reaches a terminal velocity - i.e. the speed no longer increases.
To see how this comes about, start with
where v is velocity. We'll be dealing with motion in one dimension with down being positive. At the instant the object is released, only the force of gravity acts on the body:
Air resistance gives rise to a force which acts against the direction of motion and it will depend on velocity. The exact form could be complicated but we will start with the assumption that the resistive force is proportional to velocity:
As the magnitude of velocity increases, the force due to air resistance grows and is directed upwards (negative). In this equation b is a constant but it has to have the right units so that when it is multiplied by m/sec we get the right units for mass times acceleration. The units of b work out to be kg/sec.
Ponder, for a moment, the RHS of the above equation. Initially the velocity is zero so the RHS is just the mass (m) times the gravitational acceleration (g). However, the bv term starts growing and eventually cancels the mg term at which time the net force or acceleration is zero. The velocity no longer changes and we've reached terminal velocity. The value of this terminal velocity is:
One interesting conclusion is that with air resistance present, the terminal velocity increases with mass - heavier objects will fall faster.
Let's re-write the force equation as:
where
More re-arranging:
Now integrate:
![]()
We want to solve for v(t):
![]()
Finally:
At infinite time - the exponential vanishes and the velocity is just the terminal velocity. What about for small times (just after releasing the mass)?
More below on how to expand the exponential function. So initially, the velocity grows like:
This makes sense because intially, when the velocity is near zero, there is no resistive force and we have a free fall with the velocity increasing from rest as gt.
Here is a plot of the velocity as a function of time.

![]()
Download this Interactive Physics simulation [ vt.ip.hqx ]. Use the slider bar to adject the mass of the falling mass
Series Expansion for the Exponential Function
The series expansion for the exponential function is:
It is pretty obvious from this that if you differentiate with respect to x you should get the same function back again - try it. You can also see that if x <<1 then (1 + x) is a good approximation.
What about a Resistive Force That Depends on Velocity Squared?
Suppose the resistive force looks like this:
Doing something similar to what we did above we arrive at:
where:
is constant. Now we integrate:
Here is the result:
Now solve for v in terms of t:
The function is the hyperbolic tangent. The factor in front is the terminal velocity from solving:
I used Mathematica to help me out here:


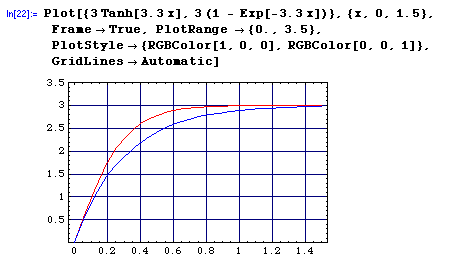
In this last step I chose the terminal velocity to be 3 m/sec with a mass of 1 kg and g = 10 m/s2. I applied this same condition to this case and the case of linear resistive force. I plot both results above. Notice that the red curve (quadratic force) reaches terminal velocity sooner that the linear case (blue curve).
Mathematica is handy indeed.