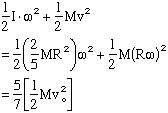Imagine striking a ball (sphere) dead center with a stick such that the center of mass of the ball gets an initial velocity v_o. At first the ball slides along the surface on which it was resting - and at first the ball does not roll. After all the initial impulse given to the ball produces no torque so the ball goes not spin.

However as the ball slides friction between the ball and the surface does two things. (1) The force of friction provides a torque causing the angular speed of the ball to increase from zero. (2) The retarding force of friction causes the center of mass velocity of the ball to decrease.

The question is - how much time is required before the ball rolls without slipping.

Note the direction of the force due to friction (f).

Let's see what happens to the velocity of the center of mass as a function of time:

and the angular velocity:

so the center of mass velocity decreases with time and the angular velocity increases (from zero) with time and when:

we have rolling without slipping and thereafter the velocity does not change.

Now let's look at the angular acceleration:

Now solve for time:

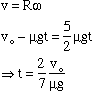
How much energy is lost to friction while the ball is slipping and rolling?

First let's calculate the final angular velocity:

Now calculate final total energy: