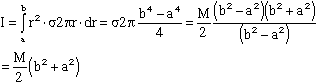Definition of Moment of Inertia
You might want to have a look at this table of moments of inertia for various objects.
Moment of Inertia of a Rod - Axes through Center
We will calculate the moment of inertia of a thin rod of length L about an axis which passes through the center of the rod and is perpendicular to the rod. The rod has mass M.

Look at the contribution of a small piece of the rod (length dx) located a distance x away from the axis. First find the mass of this piece:
Now find the moment of inertia:
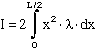
Notice that the limits of intergration are from 0 to L/2 - that's only half the rod so we multiply by 2.
Finishing up we find:
Moment of Inertia of a Rod - Axes through One End
Now let's look at this arrangement:
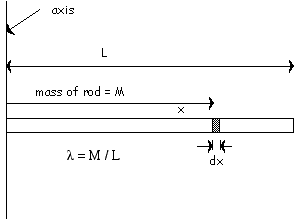
The integral now is:
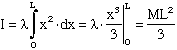
The moment of inertia is larger in this case - makes sense because there's more mass farther away from the axis than in the first case.
Moment of Inertia of a Hoop - Axes through Center
Let's find the moment of inertia of a hoop about an axis through the center of the hoop and perpendicular to the plane of the hoop. What is a hoop? Think of a hula-hoop:


All the mass is located the same distance from the origin so
Since r = R = constant I can pull it out of the integral.
Moment of Inertia of a Disk - Axes through Center
Let's now switch to a disk. Here's an example of a disk:
To find the moment of inertia of a disk, break it up into many hoops - we'll call these annuli of thickness dr as shown below.

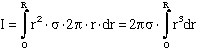
![]()
So the moment of inertia of a disk is smaller than that of a hoop of the same mass and radius - makes sense because for the hoop all the mass is as far from the axis as it can be.
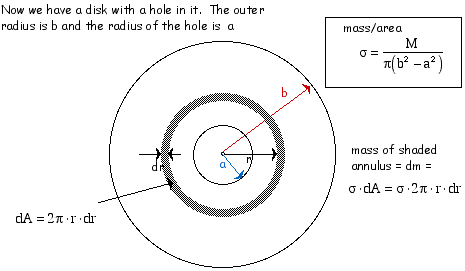
Now let's do a disk with a hole in it: