Elastic Collisions in One-Dimension
This shows two masses, one at rest, the other moving, about to have a head-on collision. The direction of the moving mass defines a direction in space. After the collision, all we can say is that the masses will move along this same direction with velocities determined by the ratio of the masses.
Let's call the mass which is initially moving the projectile and the one at rest the target.
We will call the velocities after the collision u1 and u2.
Apply momentum conservation:
and we will assume a totally elastic collision - that is, total kinetic energy is conserved:
Using these equations you can solve for u1 and u2 in terms of v1. I'll let you do the math. Here's the answer:
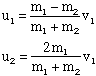
It is interesting to examine the
solutions for several special cases:
Equal masses:
In this case the projectile comes to rest after the collision and the target moves with the initial velocity of the projectile. They exchange velocities.
Suppose the projectile is much more massive than the target:
Not surprisingly, the projectile motion is pretty much unimpeded and the target moves off with twice the initial velocity of the projectile.
Now suppose the target is much more massive than the projectile - like hitting a brick wall. The projectile rebounds - with equal and opposite velocity and the target remains at rest.
Now let's look at this special case.
So if the target is 3 times the mass of the projectile, they move away with equal and opposite velocities after the collision. Suppose that we reverse the directions so that the two masses approach each other with equal and opposite velocities. After they collide, you would expect the larger mass to come to rest and the lighter one to move away with velocity v1. It's like playing a movie in reverse.
Download this movie [ collision.mov
] and play it - an
example of what we just derived.
